1. 令$A(0,a)$,$a>0$,$B(x_0,0)$上动点,连$AP$,在$AP$上找点$P$,使得$|PB|=\alpha|x_0|$,则$P$点的轨迹方程
\[(\alpha^2a^2-y^2)x^2=(a-y)^2y^2.\]
参数方程为
\[\begin{cases}x=x_0-\frac{\alpha{x_0}|x_0|}{\sqrt{a^2+x_0^2}}\\y=\frac{\alpha{a}|x_0|}{\sqrt{a^2+x_0^2}}\end{cases}\]
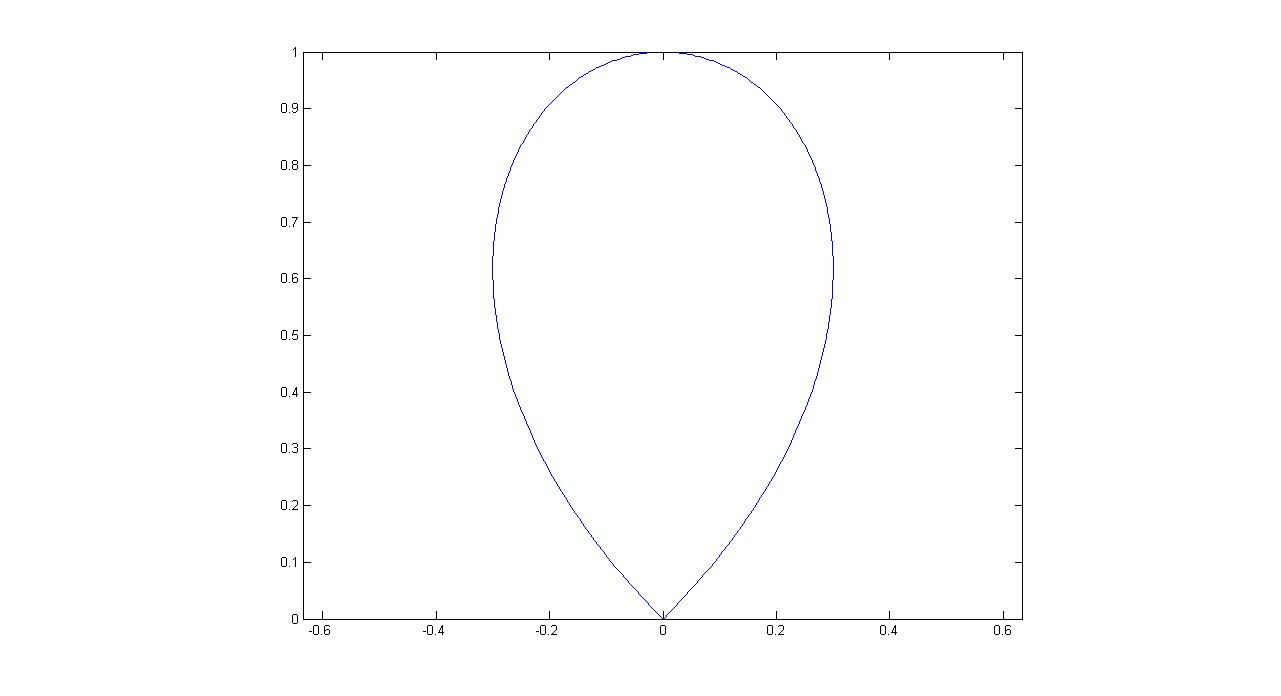
当$\alpha=1$时,轨迹方程为:
\[(a+y)x^2=(a-y)y^2.\]
图形包含的面积为$(\pi-2)a^2$.
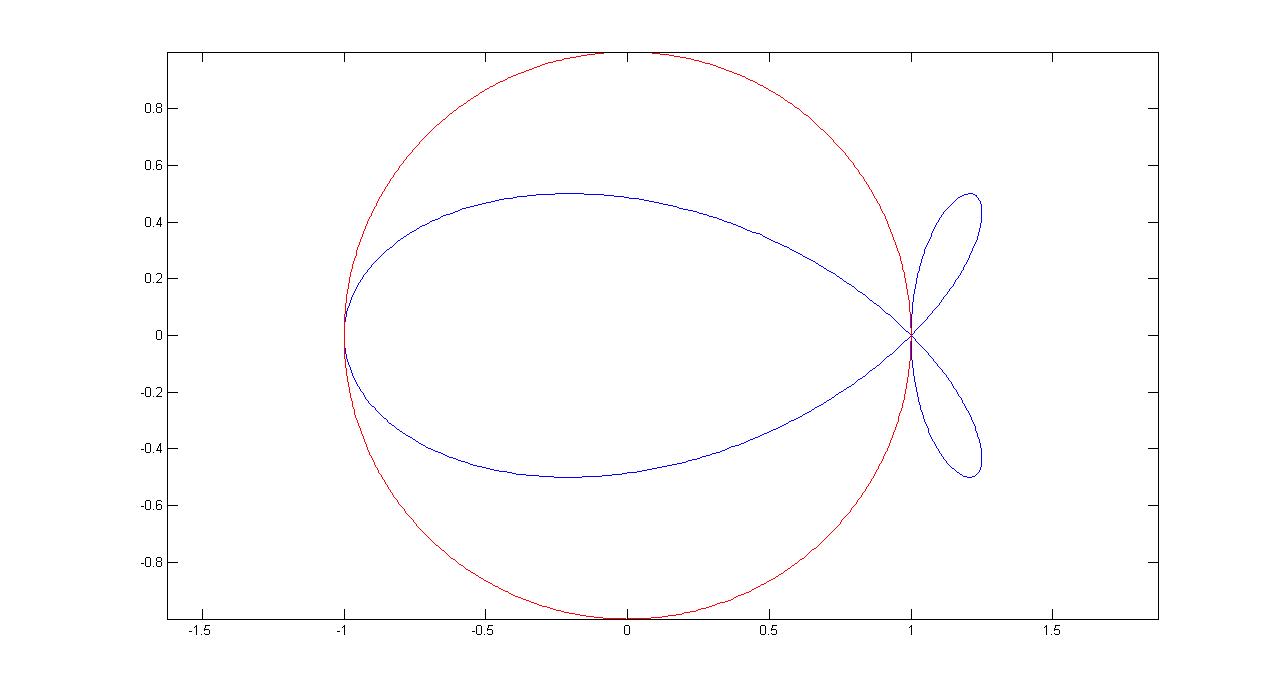
2. 圆$o$半径为$r$,圆心在原点,$A(r,0)$, $B$, $C$关于$x$轴对称,$B(r\cos\theta,r\sin\theta)$为圆$o$上动点,过$C$作$AB$连线的垂线,则垂足$P$的轨迹为
\[\begin{cases}x=r(\sin^2\theta+\cos\theta)\\y=-r\sin\theta\cos\theta\end{cases}.\]
3. 过原点作$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$在$M(a\cos\theta,b\sin\theta)$处切线的垂线,则垂足$P$的方程为
\[\begin{cases}x=\frac{ab^2\cos\theta}{a^2\sin^2\theta+b^2\cos^2\theta}\\y=\frac{a^2b\sin\theta}{a^2\sin^2\theta+b^2\cos^2\theta}\end{cases}\]

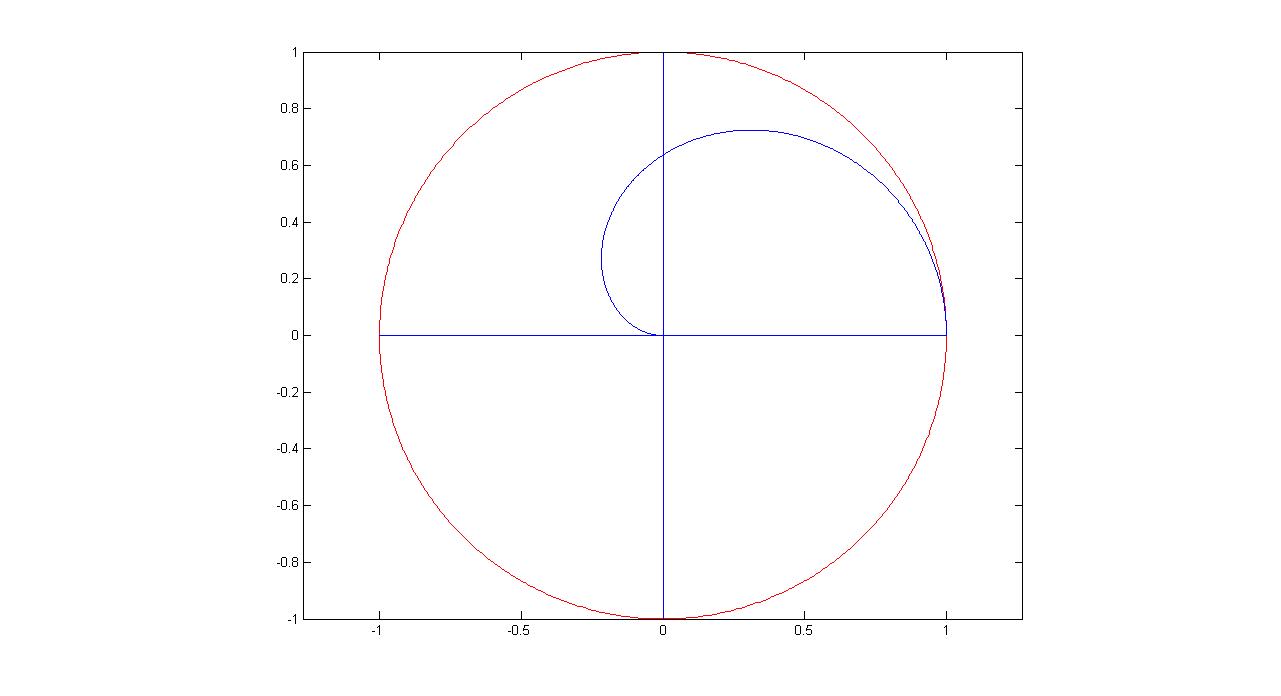
4. 圆弧半径为$r$,角度范围$[0,\theta]$,当$\theta$在$[0,2\pi]$上变化时,圆弧的重心的轨迹方程为
\[\begin{cases}x=\frac{r\sin\theta}{\theta}\\y=\frac{2r\sin^2{\frac{\theta}{2}}}{\theta}\end{cases}\]
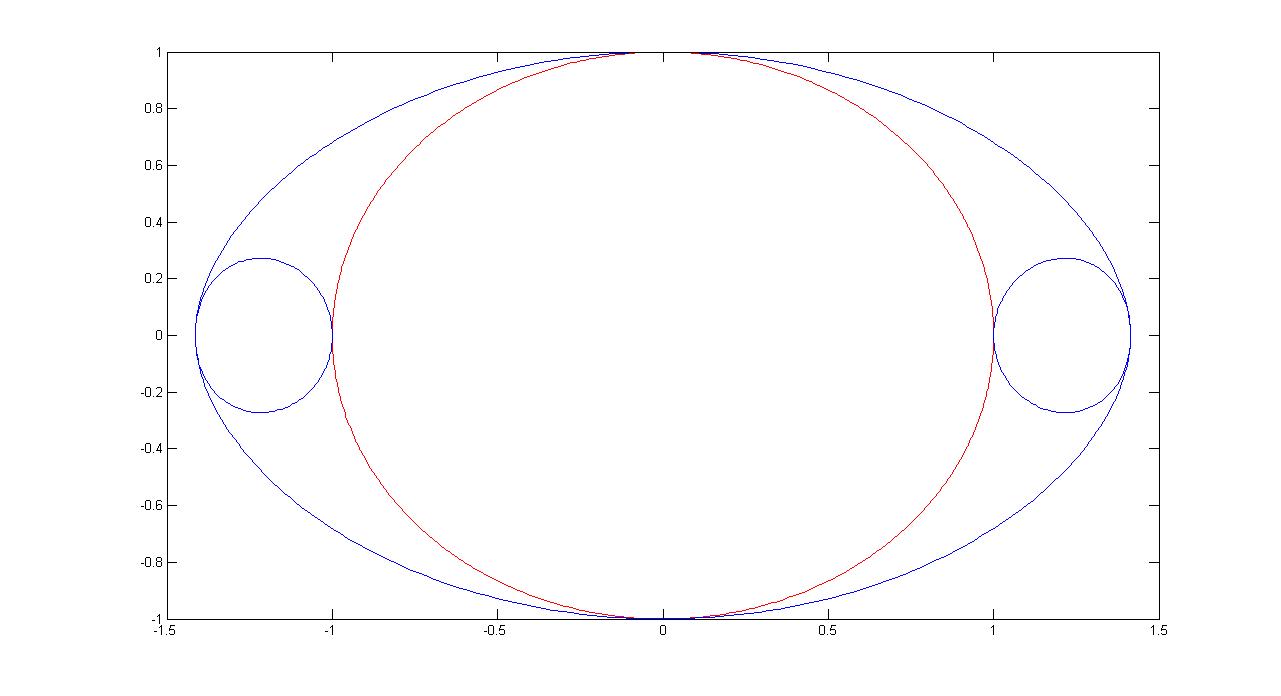
5. 圆$o$半径为$r$,$A(r\cos\theta,r\sin\theta)$为圆上动点,$B$是$A$关于$x$轴的对称点,过$B$作圆$o$在$A$点切线的垂线,垂足为$P$,其轨迹方程为
\[\begin{cases}x=r\cos\theta(1+2\sin^2\theta)\\y=r\sin\theta(1-2\cos^2\theta)\end{cases}\]
6. 圆$o$半径为$r$, $A(r\cos\theta,r\sin\theta)$为圆上动点,$AB\perp{x}$轴,$B$为垂足,过$B$分别作$Ao$和$A$处切线的垂线,垂足分别为$C$和$D$,则$C$和$D$的轨迹为
\[C:\begin{cases}x=r\cos^3\theta\\y=r\sin\theta\cos^2\theta\end{cases}\]
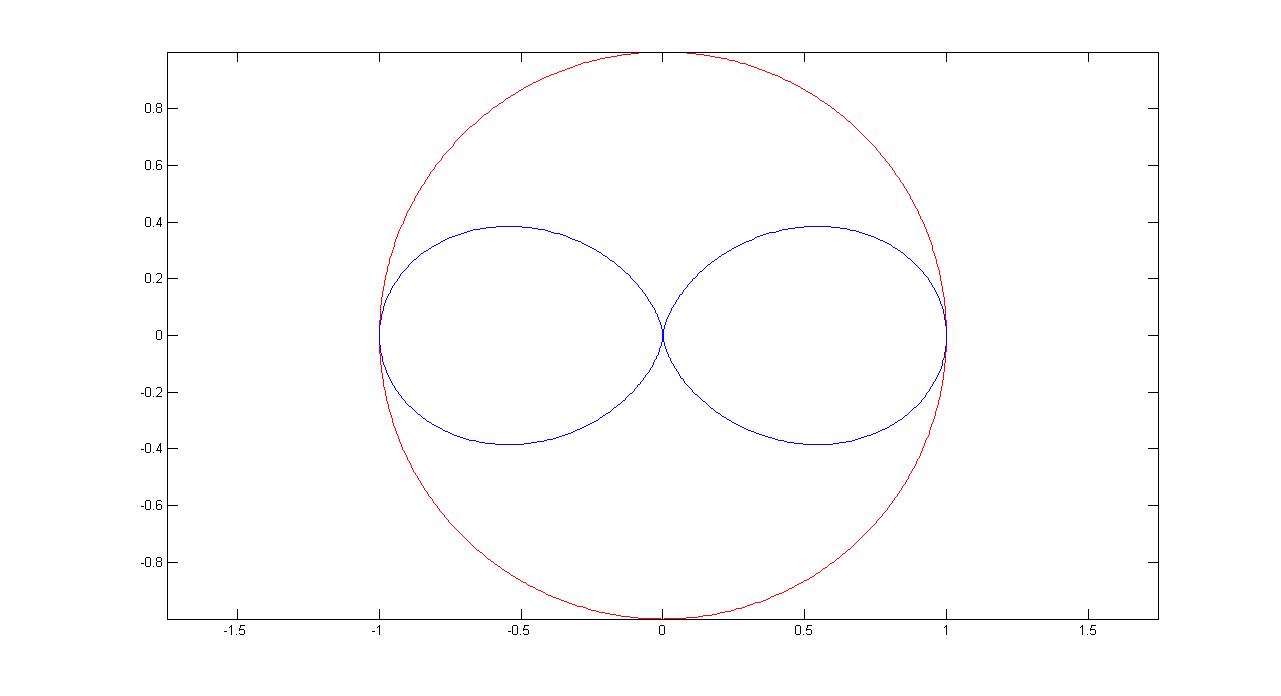
\[D:\begin{cases}x=r\cos\theta(1+\sin^2\theta)\\y=r\sin^3\theta\end{cases}\]
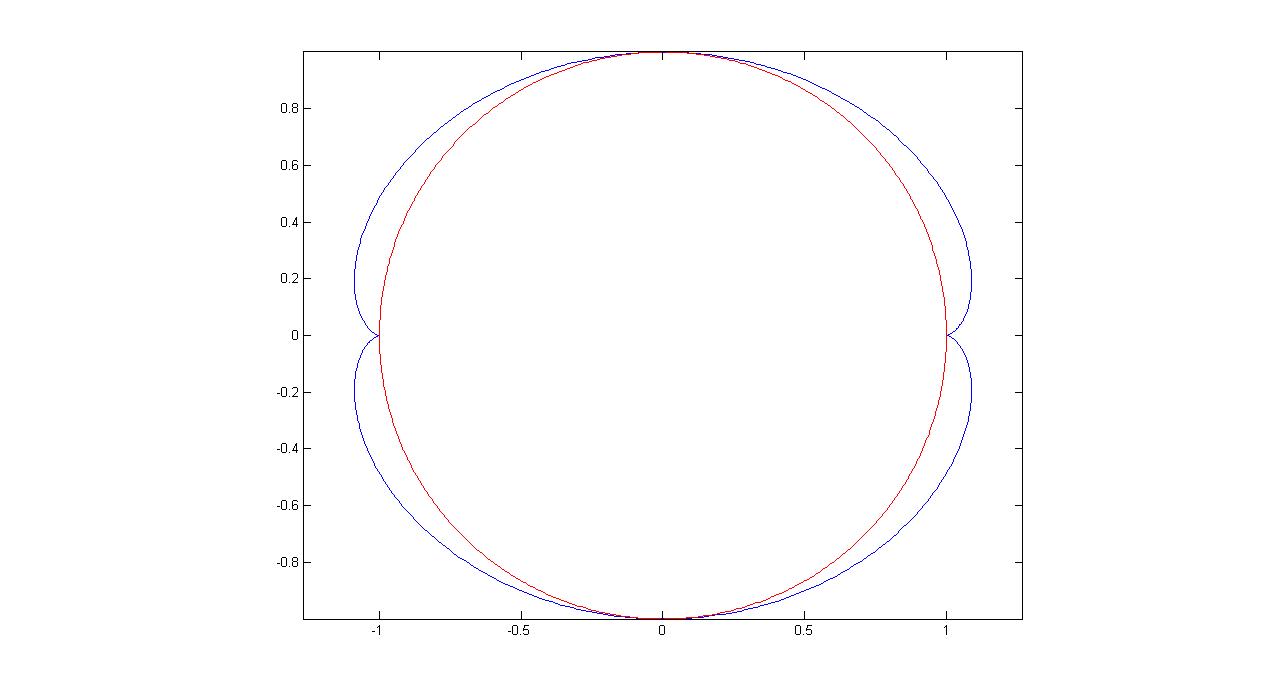
7. 圆$o$半径为$r$, $A(r\cos\theta,r\sin\theta)$为圆上动点,$AB$为直径,$C$与$B$关于$y$轴对称,过$C$作$AB$的垂线,垂足为$D$,则$D$的轨迹为
\[\begin{cases}x=r\cos\theta\cos2\theta\\y=r\sin\theta\cos2\theta\end{cases}\]
一般方程为\[(x^2+y^2)^3=r^2(x^2-y^2)^2。\]
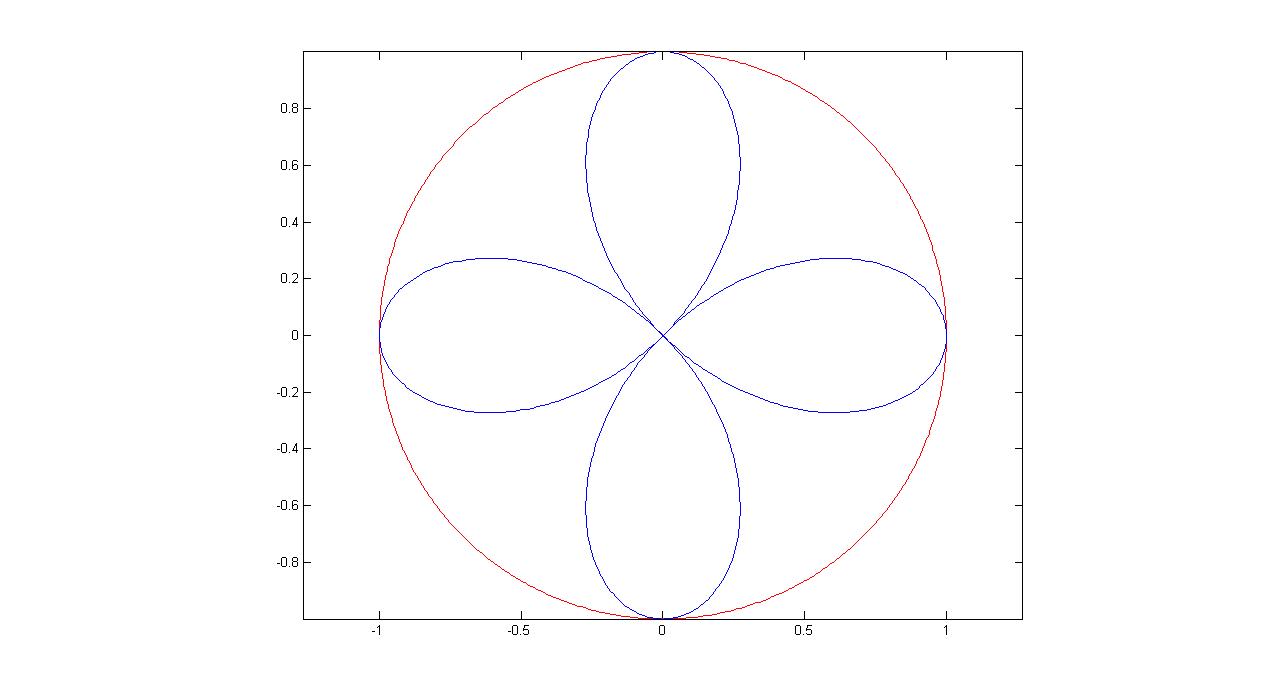
8. 圆$o$半径为$r$, $A(r\cos\theta,r\sin\theta)$为圆上的固定点,一根绳子长$s(\ge{4r})$,将绳子一端固定在$A$点,将绳子中间某点$B$沿着圆周运动,使得$AB$为圆的一条弦,绳子的另一端$C$始终垂直向下,则$C$的轨迹方程为
\[\begin{cases}x=r\cos\phi\\y=r(\sin\theta+2|\sin\frac{\theta-\phi}{2}|)-s\end{cases}\]
下面给出一些不同位置$A$点对应的$C$的轨迹
$A(r,0)$
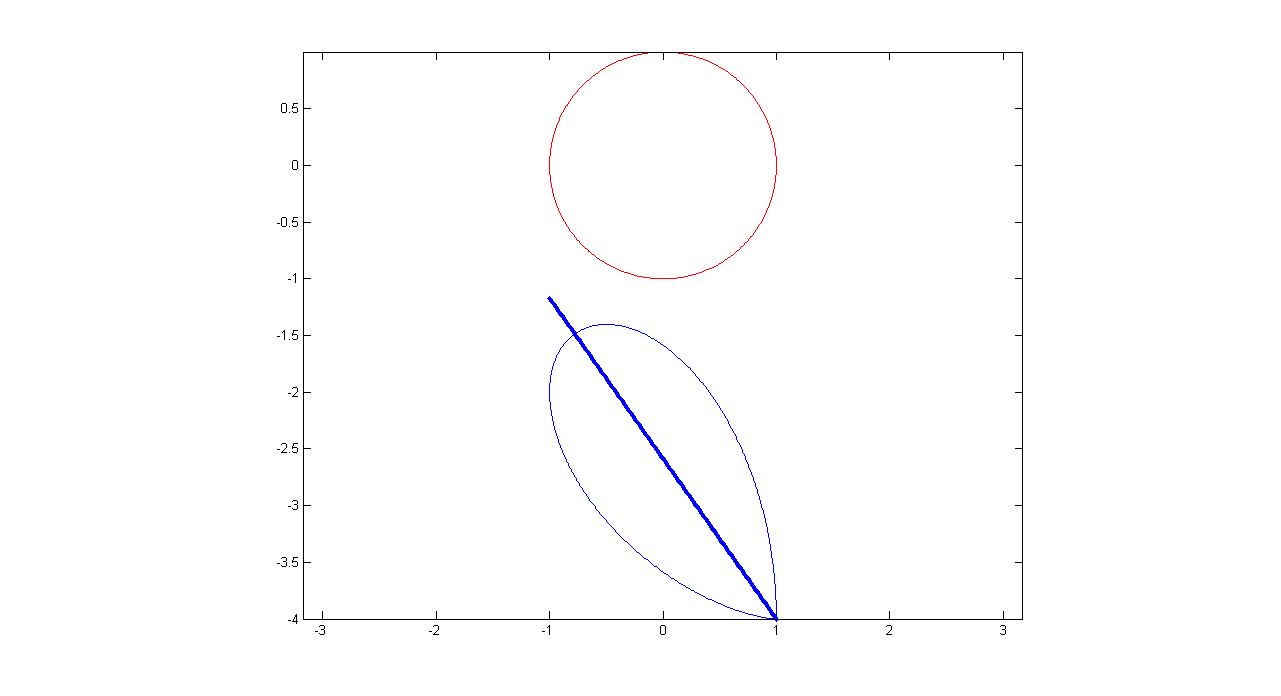
$A(0,r)$

$A(\sqrt{2}r/2,\sqrt{2}r/2)$
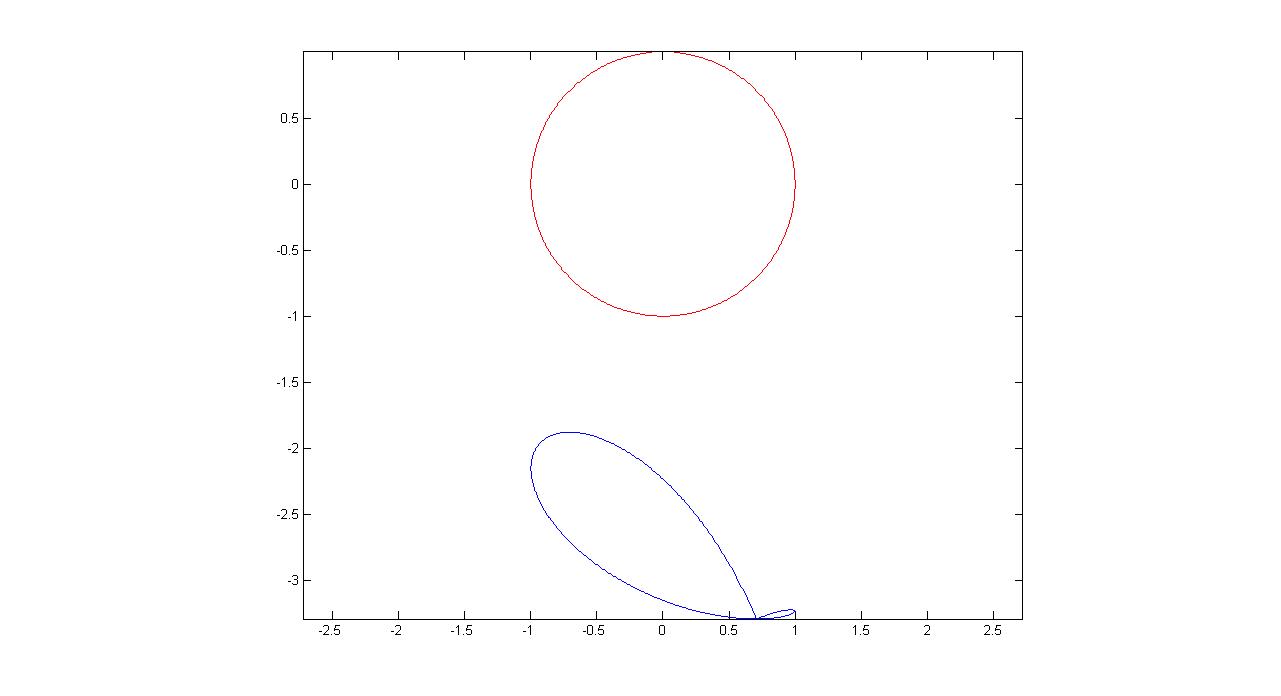
$A(0,-r)$

$A(\sqrt{2}r/2,-\sqrt{2}r/2)$
