在大多数人眼中,数学是神秘的,学数学的人是古怪的。确实,数学,特别是理论数学在现实中很少有应用之处,数学专业之外的人一生几乎都不会接触到它。那么为什么还是有很多人(此处主要指国外的)对数学研究非常痴迷呢?我想他们是爱上了数学的美吧。
此处仅举一例。著名的“费马大定理”于1995年被美国的一位数学教授Andrew Wiles证明了。他于1986年发现了证明“费马大定理”的途径,然后开始了长达7年非常艰苦的个人努力过程,期间他几乎不参加任何学术讨论,业余时间全身心投入到研究工作中。7年中只有他妻子知道他在研究“费马大定理”。最终1993年他宣布证明了“费马大定理”,后来其他数学家发现他的证明有“漏洞”,经过一年多和另一个人的共同努力,这个“漏洞”被补上,最终“费马大定理”被证明。
本文将逐一列举我所知的“数学之美”,并尽量以最通俗易懂的形式描述。由于内容一次难以写完,故本文将经常更新,如果感兴趣,欢迎经常回访。
1. Euler恒等式:$e^{i\pi}+1=0$
数学中最常见的五个量出现在一个等式中,这是多么令人惊奇!
$e$:自然对数的底,
$i$:-1的平方根,虚数单位,
$\pi$:圆周率,最常见最著名的数学常数,
$1$:万物始于一,自然数的基础,
$0$:消失,灭亡,不存在……
Euler恒等式为什么成立呢?这可由$e^x$,$\cos{x}$和$\sin{x}$的无穷级数展开得到(关于无穷级数请参考任一本高等数学教材):
\[e^x=1+x+\frac{x^2}{2!}+\cdots+\frac{x^n}{n!}+\cdots\]
\[\cos{x}=1-\frac{x^2}{2!}+\frac{x^4}{4!}-\cdots+\frac{(-1)^nx^{2n}}{(2n)!}+\cdots\]
\[\sin{x}=x-\frac{x^3}{3!}+\frac{x^5}{5!}-\cdots+\frac{(-1)^{n-1}x^{2n-1}}{(2n-1)!}+\cdots\]
可以看到,$\cos{x}$只包含$x$的偶次幂,而$\sin{x}$只包含$x$的奇次幂,而且它们的和和$e^x$有点相似,但不完全相同。由于$i$是$-1$的平方根,把它加入$e^x$的指数中,可以得到
\begin{align*}
e^{ix}=&1+ix-\frac{x^2}{2!}+\cdots+\frac{i^nx^n}{n!}+\cdots\\
=&1-\frac{x^2}{2!}+\frac{x^4}{4!}-\cdots+\frac{(-1)^nx^{2n}}{(2n)!}+\cdots\\
&+i[x-\frac{x^3}{3!}+\frac{x^5}{5!}-\cdots+\frac{(-1)^{n-1}x^{2n-1}}{(2n-1)!}+\cdots]\\
=&\cos{x}+i\sin{x}
\end{align*}
可以看到引入虚数$i$后,成立$e^{ix}=\cos{x}+i\sin{x}$。令$x=\pi$可得
\[e^{i\pi}+1=0\]
下次将介绍$1+\frac{1}{2^2}+\cdots+\frac{1}{n^2}+\cdots=\frac{\pi^2}{6}$。(2013-4-7)
2. $1+\frac{1}{2^2}+\cdots+\frac{1}{n^2}+\cdots=\frac{\pi^2}{6}$
所有自然数平方的倒数之和竟然和$\pi$扯上了关系!
Euler是历史上最伟大的数学家之一,他的名字在数学和物理领域几乎随处可见。很多深刻结论都由他发现,上面的恒等式便是其中之一。实际上,他证明了自然数偶数次幂的倒数之和的一般公式:
\[\sum\limits_{i=1}^\infty\frac{1}{i^{2n}}=\frac{(-1)^{n-1}(2\pi)^{2n}B_{2n}}{2(2n)!}\]
其中$B_{2n}$为Bernoulli数,$B_2=1/6$,$B_4=-1/30$,$B_6=1/42$,$B_8=-1/30$,$B_{10}=5/66$,$B_{12}=-691/2730$,$B_{14}=7/6$,$\cdots$。
下面说明一下Euler的思考过程。
因为
\[\sin x=x\prod\limits_{n=1}^\infty(1-\frac{x^2}{n^2\pi^2})\]
从而
\[\sin \pi{x}=\pi{x}\prod\limits_{n=1}^\infty(1-\frac{x^2}{n^2})\]
即
\[\frac{\sin \pi{x}}{\pi{x}}=\prod\limits_{n=1}^\infty(1-\frac{x^2}{n^2})(*)\]
利用$\sin{x}$的幂级数展开(见前面部分),可以得到
\[\frac{\sin \pi{x}}{\pi{x}}=1-\frac{(\pi{x})^2}{3!}+\frac{(\pi{x})^4}{5!}-\cdots+\frac{(\pi{x})^{2n-2}}{(2n-1)!}+\cdots\]
则在(*)式右端,$x$的二次幂项为$-\sum\limits_{n=1}^\infty\frac{1}{n^2}$,从而由系数相等得
\[\sum\limits_{n=1}^\infty\frac{1}{n^2}=\frac{\pi^2}{6}\]
对于一般的自然数的偶数次幂的倒数之和,也可以从上式中推出,过程比较复杂,此处从略,感兴趣的读者可以参考一些书籍。
下次将介绍$1+\frac{1}{2}+\cdots+\frac{1}{n}\sim{\ln{n}+\gamma}$。(2013-4-8)
3. $1+\frac{1}{2}+\cdots+\frac{1}{n}\sim{\ln{n}+\gamma}$
上一节中,我们得到了自然数偶次幂的倒数之和的一般表达式,对于自然数奇次幂的倒数之和还没有讨论过。结论是,自然数大于1的奇次幂的倒数之和是有限的,但是即使对于自然数的3次幂的倒数之和,也没有找到一个简单的表示,更高的奇次幂的倒数之和更是所知甚少。本节,我们讨论自然数1次幂,即自然数本身的倒数之和的问题。
因为
\begin{align*}
1+\frac{1}{2}+\cdots+\frac{1}{n}+\cdots=&1+\frac{1}{2}+(\frac{1}{3}+\frac{1}{4})+(\frac{1}{5}+\cdots+\frac{1}{8})+\cdots\\
\gt&1+\frac{1}{2}+2\times{\frac{1}{4}}+4\times{\frac{1}{8}}+\cdots\\
&=1+\frac{1}{2}+\frac{1}{2}+\cdots\rightarrow{\infty}
\end{align*}
从而调和级数$H_n=1+\frac{1}{2}+\cdots+\frac{1}{n}$是发散的,那么它增长速度多快呢?
利用微分中值定理:
\[\ln(1+\frac{1}{n})=\ln(n+1)-\ln{n}=\frac{1}{n+\theta_n}\]
其中$0< \theta_n< 1$。则有
\[\frac{1}{n+1}<\ln(1+\frac{1}{n})<\frac{1}{n}\]
对$n$从1到$k$对上式求和得:
\[\sum\limits_{n=2}^{k+1}\frac{1}{n}<\ln(k+1)<\sum\limits_{n=1}^k\frac{1}{n}\]
则
\[\ln(1+\frac{1}{k})<\sum\limits_{n=1}^k\frac{1}{n}-\ln{n}<\frac{k}{k+1}+\ln(1+\frac{1}{k})\]
令$\gamma_k=\sum\limits_{n=1}^k\frac{1}{n}-\ln{n}$,当$k\rightarrow{\infty}$时,可知
\[0< \gamma_k< 1\]
成立。又
\begin{align*}
\gamma_k-\gamma_{k-1}=&\frac{1}{k}+\ln(1-\frac{1}{k})\\
&=\frac{1}{k}-\frac{1}{k}-\frac{1}{2k^2}-\frac{1}{3k^3}-\cdots\\
&= -\frac{1}{2k^2}-\frac{1}{3k^3}-\cdots<0
\end{align*}
从而可知$\gamma_k$是单调递减的,又有界(在0到1之间),必定存在极限。令
\[\gamma_k\rightarrow{\gamma}\]
则$1+\frac{1}{2}+\cdots+\frac{1}{n}\sim{\ln{n}+\gamma}$。目前对$\gamma$所知甚少,甚至不知道它是否是无理数。对了,这个$\gamma$又是一个和Euler相关的数,被称作Euler常数。
下次将介绍阿基米德螺线。(2013-4-9)
4. 阿基米德螺线
几何中的曲线有很多,常见的圆,椭圆,双曲线等,不太常见的如摆线,螺线等。对曲线感兴趣的可以看一下我定义的一些曲线,见一些有趣的曲线。本节将介绍阿基米德螺线。
见过河螺或海螺的一定对壳上的一圈圈逐渐放大的花纹有印象。阿基米德螺线就是一种类似于那种花纹的平面曲线,见下图
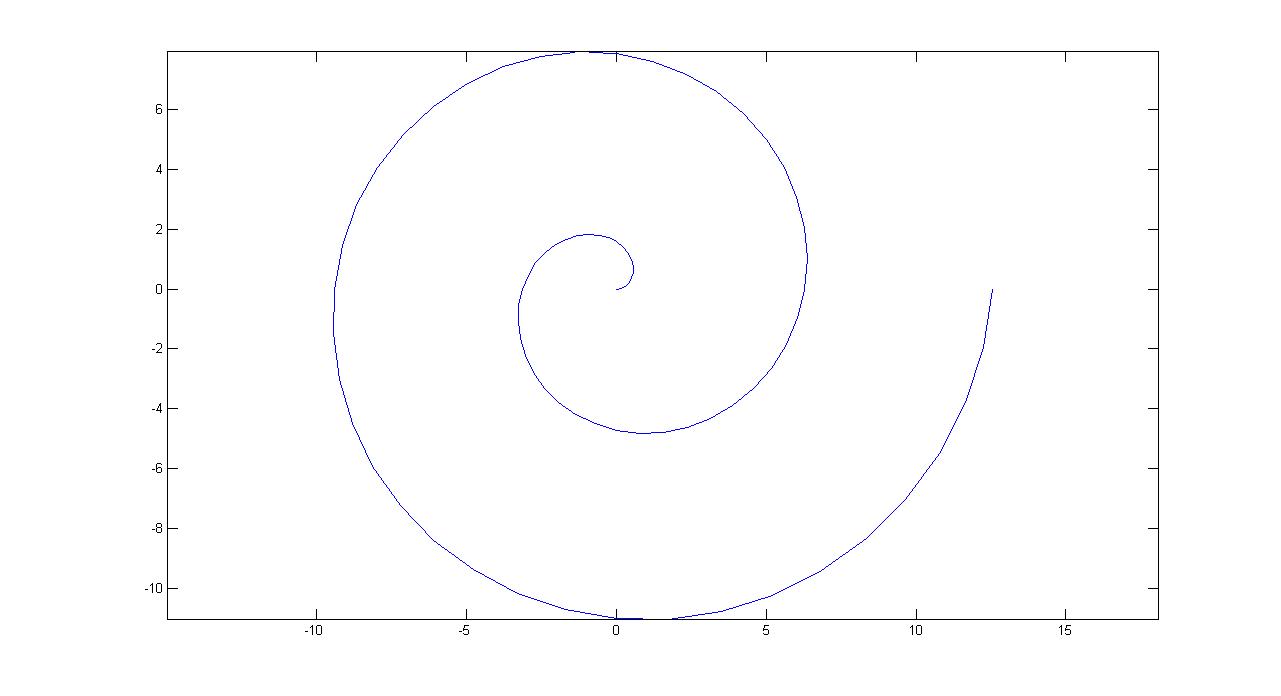
阿基米德螺线的参数方程为:
\[\begin{cases}x(\theta)=a\theta\cos\theta,\\y(\theta)=a\theta\sin\theta,\end{cases}\]
可以看到,阿基米德螺线是一种非常均匀的螺线。随着$\theta$的增大,曲线上的点在向径方向上匀速运动。
还有一种指数螺线,其参数方程为:
\[\begin{cases}x(\theta)=ab^\theta\cos\theta,\\y(\theta)=ab^\theta\sin\theta,\end{cases}\]
其中$b > 0$,图像为
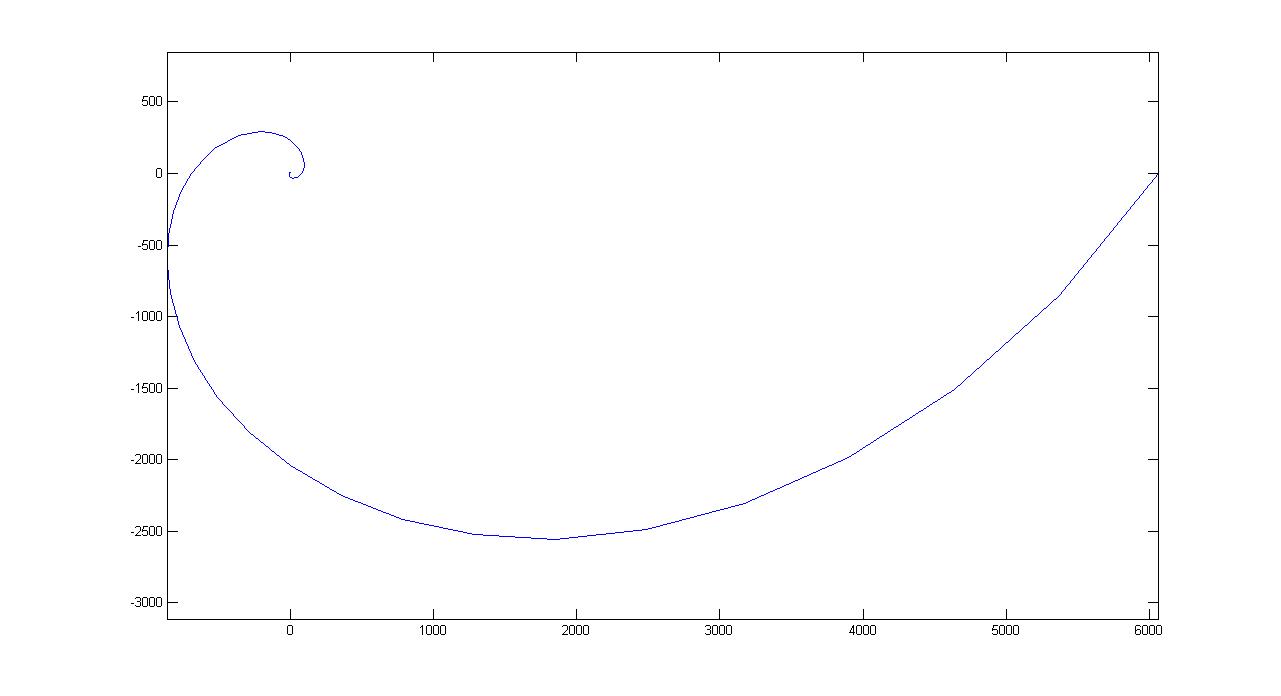
从参数方程中可以看到,指数螺线始终不会到达原点。这些曲线是不是挺有意思呢?你也可以定义自己的曲线,发挥自己的想象力吧!
下次主题先不透露,嘿嘿。(2013-04-10)
5. 尺规等分圆问题
用直尺(无刻度)和圆规可以对一个圆进行多少等分?
这个问题和前面提到的费马有一些关系。费马提出了很多猜想,其中绝大多数都是正确的,但是关于费马数的猜想确错了。费马数和圆等分问题密切相关,其定义为
\[F_n=2^{2^n}+1\]
其中$n=0,1,\cdots$,可以计算$F_0=3$,$F_1=5$,$F_2=17$,$F_3=257$,$F_4=65537$,都是素数,而$F_5$太大,费马认为它也是素数,由此他提出$F_n$都是素数的猜想。
但是到了1732年,Euler(又是他)发现$F_5=641\times{6700417}$,从而$F_5$不是素数,这说明费马的猜想错了。后来又发现$F_6$不是素数,至今通过计算机计算,共找到了243个反例,却没有再找到一个正面例子。人们开始猜想,$n>4$时,费马数全是合数。
1801年,Gauss(高斯)证明,如果费马数$k$为素数,那么可以用尺规作图将圆周$k$等分,从而对$m=2^kF_n$的$m$,若$F_n$为素数,则可以用尺规将圆周$m$等分。
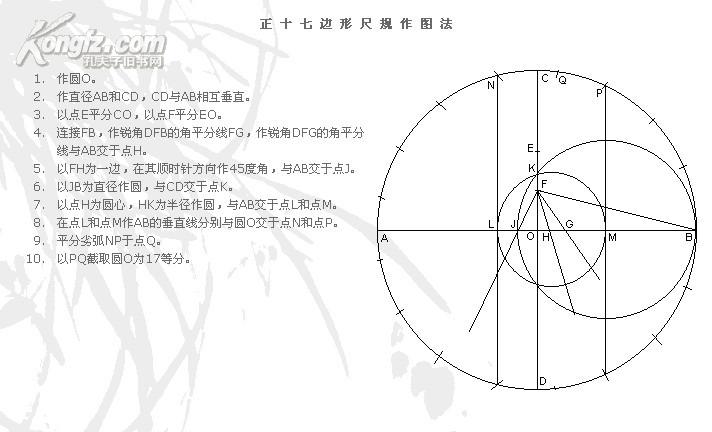
高斯根据这个定理作出了正十七边形,他是用代数的方法解决的,他也视此为生平得意之作,还交待要把正十七边形刻在他的墓碑上,但后来他的墓碑上并没有刻上十七边形,而是十七角星,因为负责刻碑的雕刻家认为,正十七边形和圆太像了,大家一定分辨不出来。
具体有关如何画出正十七边形,参考正十七边形画法
下次将介绍梅森素数。(2013-4-19)
6. 梅森素数
可以证明,在形如$F(a,k)=a^k-1$($a>1$,$k$均为正整数)的所有数中,只有当$a=2$,且$k$为素数时,$F(a,k)$才可能是素数。
如果$a>2$,则$F(a,k)=a^k-1=(a-1)(a^{k-1}+a^{k-2}+\cdots+1)$,显然不是素数。从而$a=2$。
如果$k=m\times{n}$($m$,$n$均大于1)不是素数,则$F(2,k)=2^k-1=(2^m)^n-1=(2^m-1)( (2^m)^{n-1}+(2^m)^{n-2}+\cdots+1)$,不是素数。
从而只有$k$为素数时,$2^k-1$才可能是素数。
一般记$M_p=2^p-1$,若$M_p$为素数,则称为梅森素数。当$p=2,3,5,7$时,$M_p$是素数,但$M_{11}=2047=23\times{89}$不是素数。是否有无穷多个梅森素数是数论中未解决的难题之一。截止2013年2月累计发现48个梅森素数,最大的是$p=2^57885161-1$ (即2的57885161次方减1),此时 $M_p$是一个17,425,170位数。
梅森素数的寻找非常困难,到目前为止才找到48个,这些数被称为“数海明珠”。自梅森提出其断言后,人们发现的已知最大素数几乎都是梅森素数;因此,寻找新的梅森素数的历程也就几乎等同于寻找新的最大素数的历程。
1772年,瑞士数学家欧拉在双目失明的情况下,靠心算证明了$M_{31}$是一个素数,它共有10位数,堪称当时世界上已知的最大素数。欧拉还证明了欧几里得关于完美数的定理的逆定理,即:每个偶完美数都具有形式$(2^p-1)\times{2^(p-1)}$,其中$2^p-1$是素数。
下次将介绍完全数。(2013-4-20)
7. 完全数
完全数是所有真因子的和等于自身的数,如6,它的真因子有1,2,3,而$1+2+3=6$,从而6为完全数。28也是完全数,它的真因子有1,2,4,7,14。
完全数和梅森素数有很大关系。